
PGF on Namada: public goods, capital efficiency, cool graphs - pick three

Namada's existence relies on its open-source software stack, research, and ecosystem tooling, all of which stand on the shoulders of other open-source information, readily available to the public through the internet. All of these foundations share the common attribute of being non-rivalrous and non-excludable, which are sufficient characteristics to define them as public goods.
It is a well known concept in the economics literature that public goods tend to be underfunded due to these qualities. In short, this occurs because of coordination problems between individuals, whereby equilibrium market prices do not reflect the benefit the goods existence brings to the society as a whole, but rather only the benefits received directly by buyers of the good.
It can be shown that if the consumers of the good (i.e buyers and free-loaders respectively), all merged into a single actor that made a single purchasing decision, this collective problem can be solved trivially. In economics, this imaginative all-knowing figure is sometimes referred to as the "social planner". In reality, unfortunately, merging all benefactors into one individual is not feasible, and therefore we must use other tools at our disposal to attempt to reach the same outcomes as the social planner would arrive at.
Why are public goods underfunded?
In short, it is because a single good benefits so many people at once, but usually the payment for the good cannot be coordinated in such a way where the cost is also "split" across the consumers. This means that if people could be "guaranteed" if I pay then you pay, people would be more inclined to contribute. I provide a mathematical example in the appendix for the interested reader.
Proposed solution
One proposed solution to avoid such coordination failures is to subsidise public goods in a way that allows individual incentives to align with that of the social planner. In a dream world, all public goods are well-known and all market failures can be quantified precisely. In the real world, we are not only tasked with finding public goods, but also with quantifying the total realised + potential benefit they bring over an infinite time horizon. In Namada, this simple task is assigned to a group of democratically elected individuals.
There will be a periodically elected set of stewards tasked with proposing projects/goods that should be funded. These funding proposals will pass unless they are vetoed by governance.
The stewards are responsible for two types of public goods funding:
- Continuous funding - in order to fund ongoing public goods projects in order to assist their coming to fruition
- Retroactive funding - in order to fund completed and easily evaluated public goods, in order to incentivise future public goods to be built
Funding public goods is sourced through native asset (NAM) inflation, dictated by the protocol. It is important to note that inflation here is defined as token supply increase over time, and has nothing to do with the general price level, if it was not confusing enough already.
Also note that due to being funded through NAM, an asset that is most likely not denominating the costs of providing the public goods, there is an inevitable additional frictional cost of this funding that will hopefully reduce over time as the token valuation stabilises.
At the time of writing, at least 10% of Namada annual inflation is dedicated towards PGF (although exact details of the genesis proposal remain to be finalised).
Retroactive PGF

Retroactive public goods funding (RPGF) has become an increasingly popular method for funding public goods. By retroactive, we mean to say funding goods in a post-fruition fashion. Goods receive a lump-sum subsidy in proportion to their perceived social utility at some point in time at which the perceived utility is a more accurate reflection of the realisable long-term social utility.
RPGF means to answer the question:
"What would society pay a time-traveler NOT to go back in time and destroy project A so that it doesn’t exist today (if society could coordinate)?"
The benefit of this method of PGF is that it is often more clear to evaluate the benefit public goods have brought to society after-the-fact. Because of the nature of public goods being non-excludable, its benefit to society is a function of the number of people that use it, which may not be obvious at first. Especially for public goods that have utility which is multiplicative to the number of people that make use of it (e.g the internet), retroactive funding is a useful tool. In this way, the uncertainty of the "potential utility" the good will bring under an "infinite time horizon" is greatly reduced.
The cons with retroactive PGF are two-fold:
- Retroactive PGF only allows for ex-post assessment of projects at the time the assessment is being made. This means that any public good that was unable to come to fruition because of a lack of funding or other circumstances, as well as any counterfactual of the good not existing, is ignored.
- Increased trust assumptions. In order for RPGF to correctly function as an incentive mechanism for the entrepreneur (agent) to take on risk in diverting resources to the project, the agent must be confident that the RPGF assessment mechanism will both work correctly and exist in the future at the time the assessment will be made. This may be able to be offset by some additional reward, but with risk-averse agents, this reward will have to be inefficiently allocated.
Continuous PGF
Continuous PGF (CPGF) is meant to assist public goods coming to fruition.
CPGF aims to answer the question
"What would society pay the PGF provider in order to get A in the future if all the members of society that benefit from it could coordinate?"
Every quarter, the stewards vote and decide on a group of public good projects that will receive a portion of the annual inflation distributed continuously over that quarter. The benefits of continuous funding include but is not limited to:
Cheaper as an incentive mechanism. Since the money is received up front, the entrepreneurial agent is less concerned with the possibility of not receiving funding despite the success of the project. As long as the agent is risk-averse to some degree, the total funding cost needed will be less
Increased likelihood of existing. In an economy where the entrepreneurial agent is unable to take loans at a reasonable price (either because lenders do not have enough faith in the RPGF system or because the agent is unable to provide sufficient collateral), an agent that would be unable to pursue the endeavour is more likely to pursue it.
On the other hand, there are inevitable costs:
- The Namada protocol takes on additional risk, since the benefit of the good is less clear without the benefit of hindsight.
- Unless monitoring is in place, there is a lack of incentive for commitment by the agent, which can lead to uncompleted projects. Monitoring is expensive.
- Increased uncertainty in evaluating the Steward's decisions as speculation is harder to assess. This places greater trust assumptions on the stewards acting faithfully.
Using RPGF as an incentive for future public goods
This may sound counter-intuitive, but RPGF can also act as an incentive mechanism for future public goods to come into fruition as well. Airdrops are great examples. Because there exists some probability that there will be funding in the future, people are motivated to take action today, in anticipation of perhaps reaping that reward. However, because the reward is uncertain, it can be modelled in the same way as a risky investment.
Looking at RPGF in this light, we can see that depending on how "risk-averse" the public goods producer is, the amount of RPGF needed to motivate them will differ. The below graph depicts the additional amount of funding needed in RPGF in order to motivate agents with various "risk-profiles". The mathematics behind this can be found in the appendix.
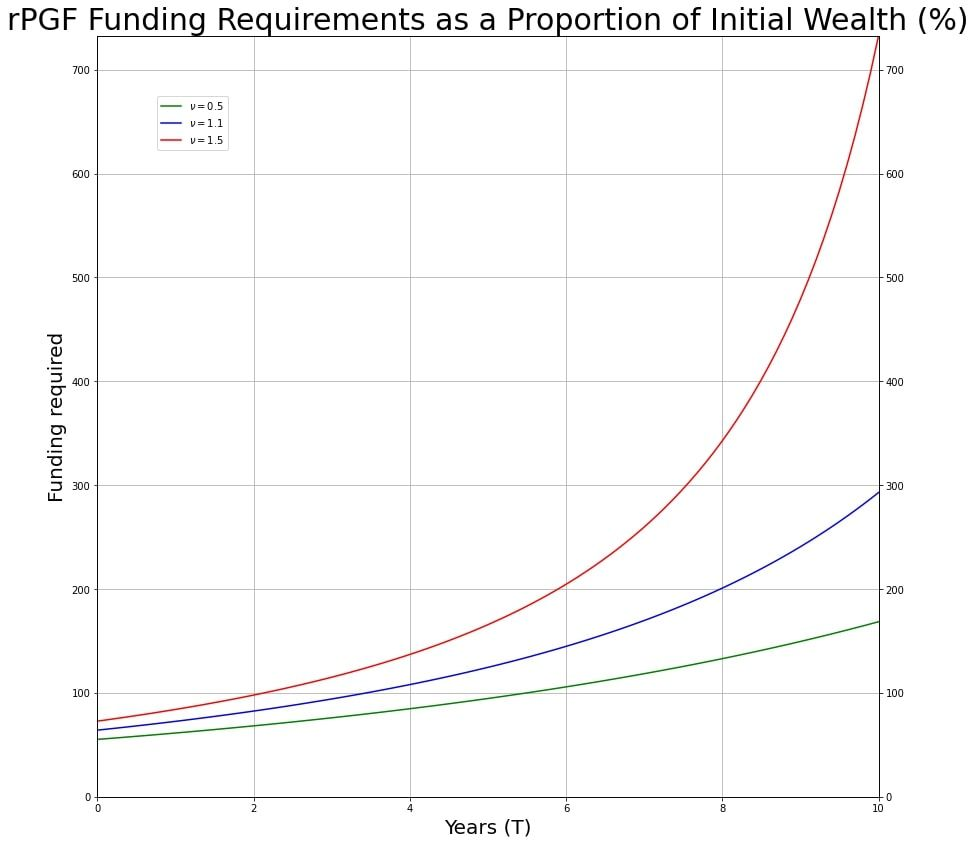
To understand the graph more precisely, the explanation in the appendix will be needed, but in short, the red line shows the amount of funding needed for the most risk-averse agent, and the green line shows the amount of funding needed for the least risk-averse agent.
It may be interesting to consider that the risk-profiles in the blockchain-space may not be as high as that in the general population ...
PGF implemented on Namada
PGF Stewards
Genesis
The genesis block proposed by the Anoma Foundation (AF) will include an initial PGF set of stewards. These stewards will serve to direct funding to public goods up until the point that there is a governance vote to remove them as stewards (or if one of their proposals gets vetoed or if they resign). New Stewards can be elected by governance through governance proposals.
Electing new PGF Stewards
The full technicalities of electing new PGF stewards can be found in the specs, but to summarise, the set can consist of any arbitrary number of stewards, that coordinate offline to make transparent proposal transactions for either CPGF or RPGF. In order to become elected, a steward address must be proposed and voted on by governance. Proposed PGF Steward becomes elected if and only if at least $\frac{1}{3}$ of all governance voting-power voted Yay on the proposal.
Voting-out PGF Stewards
In a similar way, PGF proposals can be created that aim to "vote-out" a current PGF Steward. The rules that dictate if this proposal is executed is identical to that of electing in a new Steward.
Funding public goods
The elected pgf-stewards can then unilaterally propose PGF transactions of either CPGF or RPGF form. A CPGF transaction will send a pre-determined amount of NAM each epoch to a specified recipient address. An RPGF transaction is a simple transfer of NAM.
Any such funding proposal is proposed to governance, and may or may not be vetoed if people disagreed with the funding decision.
The responsibilities of the PGF Stewards
Being a PGF Steward comes with a great responsibility. The stewards are entrusted with directing token supply inflation, the cost of which is born by the users of Namada, towards projects that are indeed valued by the Namada ecosystem.
Evaluating projects is a difficult task, and the stewards will have to figure out a reasonable cadence at which to self-evaluate their funding streams. Given that all PGF will be denominated in NAM, which will fluctuate in value (as denominated in the cost of the projects in which they are funding, which will usually be denominated in another currency such as USD/EUR/GBP/CNY/JPY etc) this evaluation will prove additionally difficult. We expect the PGF stewards to propose adjustments to funding over time, perhaps giving multiple rounds of RPGF to the same projects if they realise the initial funding was small in proportion to the value/cost ratio of the project. For CPGF, we expect "streams" of funding to both be increased and decreased over time, depending on how the estimate of the public value changes with time.
The PGF stewards will also be responsible for communicating with the recipients of the PGF in order to ensure the funds are received appropriately.
In addition to this, the PGF stewards are expected to act out of selfless interest, avoiding the temptations of being lobbied or "rent-seeked". We expect that some of such behaviour may occur, but believe that good-faith, steward-to-steward accountability (given the set of stewards is sufficiently decentralised in interests), as well as the veto mechanism through governance will act as a sufficient backstop to this.
Compensation of the PGF Stewards
For the reasons outlined above, the PGF stewards experience costs that should be compensated. For this reason, Namada allocates a pre-specified amount of token supply inflation such that the stewards can be compensated.
The genesis RPGF and CPGF round
In addition to the stewards elected at genesis, the Anoma Foundation (AF) will propose a curated list of RPGF and CPGF recipients that will receive a minimum of 20% of initial NAM token supply. To see all of the RPGF nominations made thus far, see https://forum.namada.net
Four goals of PGF (WIP)
Public goods funding on Namada is intended to be directed to the four following categories. The Stewards will be responsible for providing reasonable evidence to justify their funding decisions in terms of these categories.
For development related to Namada/Anoma ecosystem:
- Technical research related to Namada/Anoma, e.g research in cryptography, distributed systems, consensus mechanisms, etc.
- Engineering related to Namada/Anoma, including but not limited to the user-interface, storage/throughput optimisation, bug-fixes and can be distrubted through e.g developer grants, bug bounties, etc.
- Social research & art related to Namada/Anoma, more specifically resarch exploring the relationship by the technology and humans. This may be how shielding affects interactions e.g artist grants etc, and may also concern interactions with the legal and policy spheres.
For public goods not directly related to Namada/Anoma:
- External public goods - e.g carbon capture, independent journalism, direct cash transfers, etc.
More detailed information can be found in the specs.
Note
It is important to note that, as with most protocol parameters on Namada, these four funding categories are not set in stone. Instead, they are expected to change over time (through Governance proposals) as a way of re-chartering the ends to which the means of public goods funding are intended to meet.
Conclusion
We hope we have provided sufficient motivation as to why we should fund public goods and why the we can't expect the "invisible hand of the free-market" to provide enough of the good on its own. Granted, no money is free, but we believe that funding these goods is essential for a sustainable future of free open source software and open research that Namada and similar systems will inevitably rely upon.
In short, the Namada protocol aims to fund public goods divided into four categories: technical research, engineering, social research and external public goods. It aims to accomplish this endeavour through two means: continuous and retroactive public goods funding. There will be elected (hopefully) human stewards that will make these funding decisions, and will be compensated for their efforts.
In addition to the PGF Stewards, there will be a list of projects receiving retroactive public goods funding at genesis.
All of what we have discussed requires input from public-goods enthusiasts like yourself, so please share your voice in the forum, as we would love to hear any questions, concerns, recommendations and projects you believe are viable candidates to receive funding!
Appendix - The Maths
A mathematically motivated public good example
Here is a short example to demonstrate the market failures of public goods funding in the free market.
Let’s simplify the world where we have a public good of free open source software. Let the number of blocks committed towards this project be denoted by $x$. Assume that each additional block of code committed provides the end user with $(100 - x)$ additional “monies” of benefit, and costs the developer $x$ “monies” to commit.
To put this in as obvious a manner as possible we have
$$ D_i = (100 - x) $$
$$ S = x $$
Where $D_i$ denotes "individual demand", also known as "marginal benefit" to the consumer, and $S$ denotes the "supply" or the "marginal cost" to the producer.
When we have individuals coordinate in the free-market, the 50th line of code is provided at a cost of $100 - x = x \Rightarrow x = 50$ monies. In equilibrium we have 50 blocks of code at 50 monies each, costing society a total of 2500 monies for a benefit of (99 + 98 + 97 + ... 50 =) 3725 monies per user.
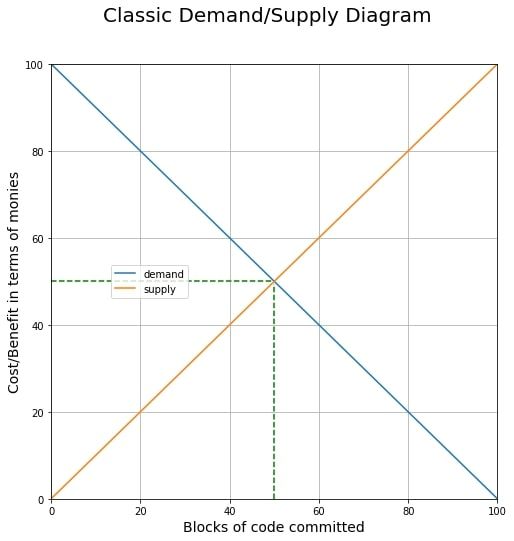
Let's say there are $N>100$ users. Now what would happen if they could all commit to "splitting the bill" before-hand?
This means that each additional line of code now costs them $\frac{x}{N}$ monies rather than $x$.
$$ 100 - x = \frac{x}{N} => x = \frac{100}{1+\frac{1}{N}}$$
As $N \rightarrow \infty$, we start to arrive at a social solution with the maximum number of blocks of code committed.
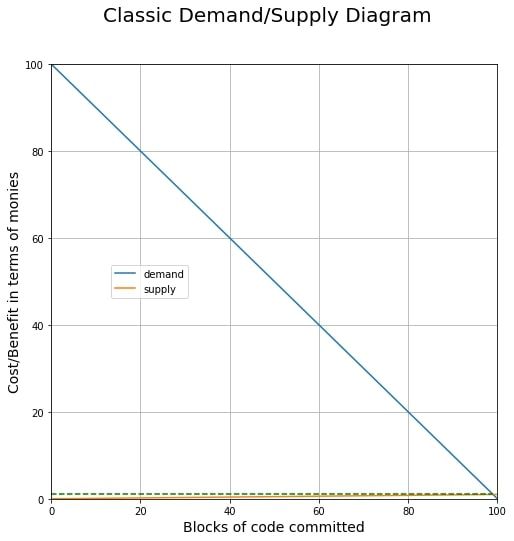
What economic tool do we have at our disposal that forces people to "split the bill" amongst all the money holders?
Hint: It starts with "i" and ends with "inflation". (And from here on we use "inflation" to mean money supply increase, which is related to but not synonymous with general price level increase, which is what inflation is known as to many economists. Here by "inflation" we simply mean an increase in NAM token supply over time).
Mathematically determining the right amount of funding
Assumptions
When doing economic modelling, there will inevitably be a number of assumptions. I will attempt to outline them carefully here.
1. Rational agent
One of the greatest assumptions we tend to make is that the agent is rational. In this sense, we mean an agent that is able to perfectly determine its preferences over any two alternatives in such a way that if the agent were given all the alternatives the universe had to offer, the agent would be able to rank them from "most preferred" to "least preferred".
2. Risk neutral agent (relaxed later)
This means that the agent is trying to maximise the reward in expectation. A risk-averse agent will inevitably require more funding.
3. Risk free interest rate
We will assume a risk-free interest rate $r$ that remains constant over time. This is a very silly but simplifying assumption. It is arguably silly for the reason that it's hard to imagine that a "risk-free" way of making money even exists, so this "risk-free" is always relative to something, and further that it remains constant is likely impossible. A changing $r$ can easily be incorporated at the cost of uglier looking equations.
4. Known probability of receiving funding
The rational agent is able to accurately assess the probability of receiving funding at time $t=T$ to be $s$.
5. The public good's benefit to society is great enough
Additionally, we assume that the ex-post benefit to society $U$ at the time of assessment $T$ is greater than the cost of investing in the project (so that funding entity - in this case Namada - will find it worth funding ex-post). I.e
$$ U_{society}(\text{public good}, t=T) > C(1+r)^T$$
Scenario
The agent is considering investing in a public goods project. The agent assesses the probability of the project being successfully funded by the RPGF funding entity at some rate $0<s<1$. Note that the success rate $s$ includes both
- The inherent risk of the project itself as well as
- The risk attached to the RPGF funding entity existing and functioning properly at the time of assessment.
The project comes at one-time sunk cost $C$, which includes the opportunity cost to the agent of choosing this endeavour over any other in addition to any other non-monetary cost to the agent.
$$\mathbb{E}[\text{Funding} - \text{Costs}] > 0 \Rightarrow
\mathbb{E}[sF - C(1+r)^T]> 0$$
An agent will be incentivised to invest in their project if funding retroactively directed to the project $F$ is at least as high as their costs.
$$ sF \geq C(1+r)^T \Rightarrow F \geq \frac{C}{s}(1+r)^T $$
If the agent is risk-averse, then this becomes more complicated. A common way to measure risk aversion is to assign the agent a utility function
$$u(c) = \begin{cases}
\frac{c^{1-\eta}}{1-\eta} &\text{if }\eta \geq 0 \text{ and } \eta \neq 1\
\ln(c) &\text{if } \eta = 1
\end{cases}$$
(known as isoelastic utility).
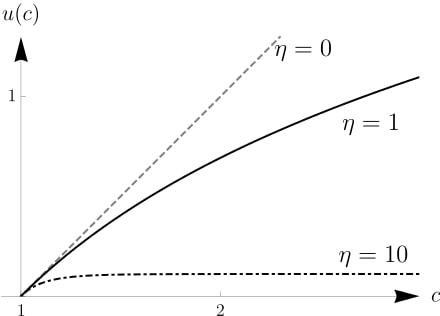
In non-nonsense speak, this basically means that the agent is sensitive to uncertainty, and this risk-averseness is captured by $\eta \geq 0 \text{ } \eta \neq 1$.The bigger the $\eta$, the bigger the adversity to risk. Importantly, this aversion to risk means that the agent must receive a greater amount of funding in order to compensate for her distaste for uncertainty. This additional funding requirement is often referred to as a risk premium.
For the case $\eta = 1$, doubling the expected reward increases the utility of the risk-adverse agent only by a additive constant. More concretely, if Alice has the choice between 100 dollars with certainty or flipping a coin to win $x$ dollars, she would need at least $x=10000$ dollars for the coin flip to be worth the trouble.
For the RPGF example, then we have
$$ \mathbb{E}[u(\text{Funding + Endowment - Costs})] > u(\text{Endowment}) \Rightarrow $$
$$ s\frac{(E + F - C(1+r)^T) {1-\eta}}{1-\eta} + (1-s)\frac{(E - C(1+r)^T){1-\eta}}{1-\eta} \geq \frac{E^{1-\eta}}{1-\eta} $$
$$ \Rightarrow $$
$$ F \geq \big(\frac{E^{1-\eta} - (E - C(1+r)^T){1-\eta}(1-s)}{s}\big)^\frac{1}{1-\eta} - (E - C(1+r)^T) $$
Where $E$ is some initial endowment for the agent (if you start off wealthy, you can take more risks, but that's a topic for another discussion).
We can analyse that the amount of funding required for an agent operating under this utility function to find the investment worthwhile will be greater than a risk neutral agent's preference if and only if $\eta \geq 0$.
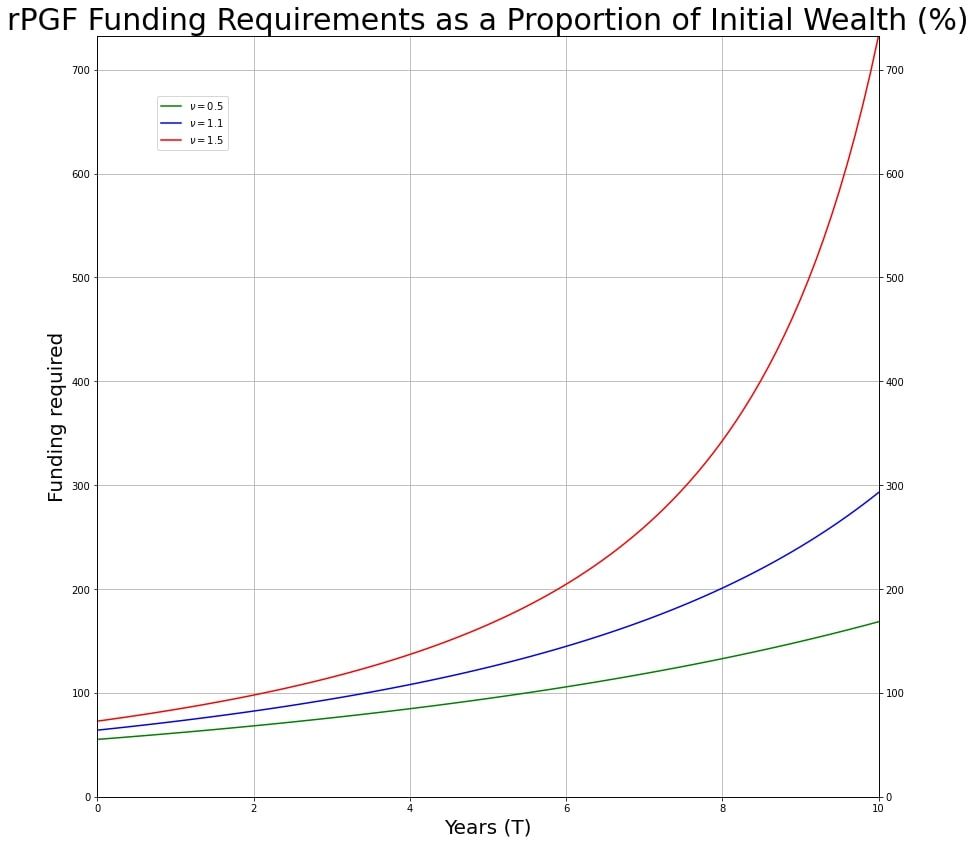
The above image depicts the funding requirements (as a proportion of initial wealth) required for agents with varying risk profiles, assuming the cost of the project is $10 \text{%}$ of their initial wealth and the probability of receiving funding is $20 \text{%}$. As the probability of receiving funding decreases, the required funding increases by a magnitude dictated by their risk adversity.
There is an extensive literature in estimating $\rho$, and estimates vary wildly. Groom and Maddison estimated the value to be around 1.5 for the United Kingdom. But of course, this number may easily overestimate risk adversity for certain relevant groups ... 💎🙌🦍🤝💪📈.
Ponder
We assumed that $\eta \geq 0$, but what is the risk profile of someone with $\eta < 0$?
How does this change the amount of required funding?
In a risk averse world, therefore, it is important to establish confidence in agents that RPGF works and that it works well. As $s$ approaches $1$, we begin to move towards a world where retroactive funding achieves all of the benefits of continuous funding, whilst also maintaining its advantage of filtering uncertainty at no additional premium (since if F is large enough this is true regardless). The premium needed whilst $s<1$ will depend on the risk-averseness of the agent, and could be mitigated by the existence of insurance, should a market for that exist.
